1870. Тестирование шаффл-машин

У Сергея Михайловича очень интересная работа. Он занимается тестированием шаффл-машин – механизмов, используемых для тасования стопок карточек.

Машины, которые тестирует Сергей Михайлович, осуществляют перестановку стопок из n карточек, где n – чётное натуральное число. Механизм, по которому они работают, состоит в применении к исходной стопке определённой последовательности преобразований, каждое из которых имеет один из двух типов – U или D.

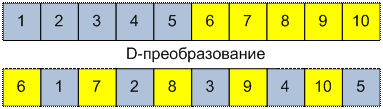
U-преобразование производится следующим образом. Сначала исходная стопка из n карточек делится на две части, первая из которых состоит из n/2 верхних карточек, а вторая – из n/2 нижних. Затем в результирующую стопку поочерёдно помещается по одной карточке из каждой из двух частей, начиная с первой. D-преобразование отличается от U-преобразования только тем, что на втором шаге результирующая стопка начинает формироваться, начиная не с первой части, а со второй.

Если мы пронумеруем карточки сверху вниз числами 1, 2, ..., n, то в результате U-преобразования карточки будут следовать сверху вниз в порядке 1, n/2 + 1, 2, n/2 + 2, ..., n/2, n, а в результате D-преобразования порядок карточек будет таким: n/2 + 1, 1, n/2 + 2, 2, ..., n, n/2.

Сергей Михайлович проводит тестирование следующим образом. Он берёт n карточек, пронумерованных от 1 до n, и формирует из них стопку так, чтобы номера карточек в стопке возрастали при их просмотре сверху вниз. Затем он помещает стопку в машину и производит её перетасовку. После этого Сергей Михайлович достает из результирующей стопки k-ю сверху карточку и в зависимости от её номера делает вывод об исправности или неисправности тестируемой машины.

Для ускорения процесса тестирования Сергею Михайловичу нужна программа, вычисляющая, чему будет равен номер k-й сверху карточки в результирующей стопке, если шаффл-машина работает корректно.

Вход. Первая строка ввода содержит целые числа n и k (1 ≤ k ≤ n ≤ 2000000000, число n – чётное). Во второй строке записано от 1 до 1000 символов 'U' и 'D' без пробелов. Эти символы описывают последовательность преобразований, применяемых машиной для перестановки карточек. Символ 'U' соответствует U-преобразованию, а символ 'D' – D-преобразованию.

Выход. Единственная строка вывода должна содержать одно целое число – номер k-й сверху карточки в результирующей стопке, считая с единицы.

Пример входа	Пример выхода
20 7 DUUUDUDUDU	1

РЕШЕНИЕ

моделирование

Анализ алгоритма

Рассмотрим U-преобразование. Если i Î {1, 2,…, n / 2}, то U(i) = 2i – 1, U(n/2 + i) = 2i.

Равенство U(a) = b означает, что карточка с позиции a перемещается на позицию b.

Рассмотрим D-преобразование. Если i Î {1, 2,…, n / 2}, то D(i) = 2i, D(n/2 + i) = 2i – 1.

Для решения задачи следует промоделировать тасование карт в обратном направлении. Зная k-ый номер сверху карточки по окнончанию тасования, можно за O(n) найти ее расположение в колоде перед тасованием. Выведем формулы обратных преобразований:

Если i четно, что U^-1(i) = n/2 + i/2. Если i нечетно, что U^-1(i) = (i + 1)/2.

Если i четно, что D^-1(i) = i/2. Если i нечетно, что D^-1(i) = n/2 + (i + 1) /2.

Реализация алгоритма

Реализуем функции Uinv и Dinv, обратные преобразованиям U и D.

int Uinv(int i)

{

if (i % 2) return (i + 1) / 2; else return n / 2 + i / 2;

}

int Dinv(int i)

{

if (i % 2) return n / 2 + (i + 1) / 2; else return i / 2;

}

Читаем входные данные. Проходим по строке преобразований справа налево и последовательно производим обратные преобразования.

scanf("%d %d\n",&n,&k);

gets(s); len = strlen(s);

for(i = len - 1; i >= 0; i--)

{

if (s[i] == 'U') k = Uinv(k);

else k = Dinv(k);

}

printf("%d\n",k);